The Electromagnetic Shielding Effectiveness Comparison of Stainless-Steel Wire Mesh and Brass Wire Mesh
Metal mesh is widely used in electromagnetic shield engineering due to its obvious advantages, such as ventilation and effective lighting. In this paper, Hightop® Metal Mesh will explain the shielding mechanism of the wire mesh, as well as analyze and compare the electromagnetic shielding effectiveness of both stainless-steel wire mesh and brass wire mesh in the far field both in theoretical methods and in lab tests.
1. Shielding Mechanism of Wire Mesh
1.1. Electromagnetic shielding is used to restrict the transfer of electromagnetic energy from one side of the shielding material to the other. Typically expressed by shielding effectiveness (SE).
The shielding effectiveness is the ratio of the incident or emitted electromagnetic wave to the reflected or transmitted electromagnetic wave after being shielded in the same place. This is the attenuation value of the shielding material to the electromagnetic signal. The unit is expressed in decibels (dB), which can be written as the following equation:
Formula 1
SE = 20lg (Eb/Ea), Eb and Ea is the electric field strength before and after shielding;
SE = 20lg (Hb/Ha), Hb and Ha is the magnetic field strength before and after shielding;
SE = 20lg (Pb/Pa), Pb and Pa is the intensity of the energy field before and after shielding.
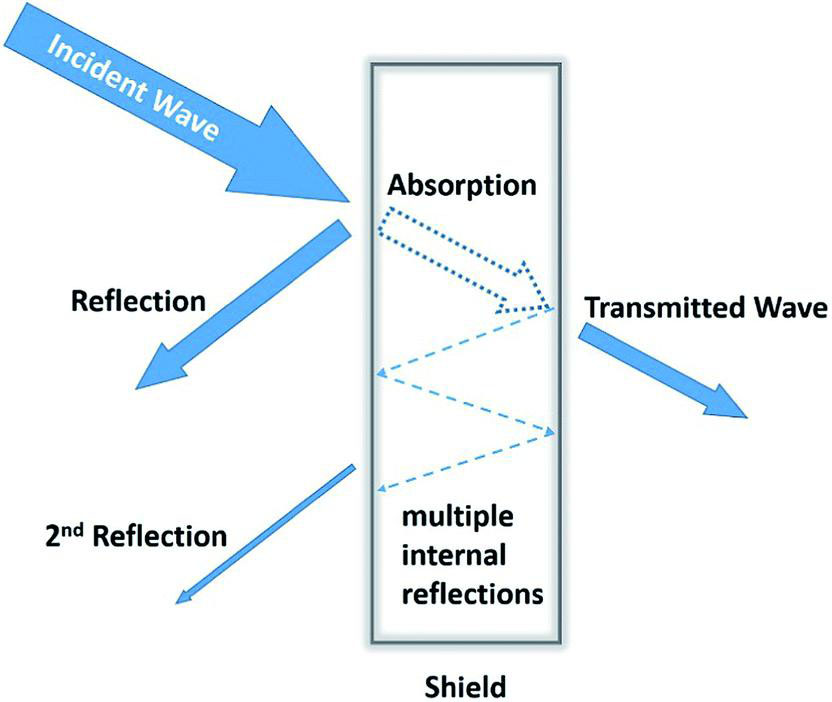
When electromagnetic waves reach the surface of the shielding material, there are usually three different attenuation mechanisms:
- R: Reflection Attenuation: When the electromagnetic wave reaches the surface of the shielding material, the single reflection attenuation of the electromagnetic wave is caused by the abrupt change of the wave impedance;
- A: Absorption Attenuation: The electromagnetic waves that are not reflected by the shielding material and enter the interior of the shielding material are continuously absorbed and attenuated by the shielding material。
- B: Multiple Internal Reflections Attenuation: The electromagnetic waves that have not been absorbed and attenuated inside the shielding material are attenuated by multiple reflections between the two interfaces of the shield.
1.2. The total shielding effectiveness of electromagnetic waves through shielding materials can be calculated as follows:
Formula 2
SE = A+B+R
The larger the attenuation value, the better the shielding effectiveness.
1.3. In addition, considering the difference between the wire mesh and the metal sheet, it should also involve the correction coefficient of the number of meshes per unit area (K1), the correction coefficient of low-frequency penetration (K2), and the correction coefficient of the mutual influence between adjacent meshes (K3). Thus, there are a total of six factors. The shielding effectiveness calculation formula can be written as:
Formula 3
SE = A+B+R+K1+K2+K3
The items in Formula 3 are now described as follows:
A: The absorption attenuation is related to the hole shape of the wire mesh. For rectangular holes:
Formula 4
A = 27.3t/w
In Formula 4, “t” is the depth of the hole in cm, and “w” is the wide side length of the rectangular hole perpendicular to the incident field in cm.
R: The reflection attenuation depends on the ratio of the wave impedance in the hole to the impedance of the incident wave. For rectangular holes:
Formula 5
R = 20lg [(1+N2)/4N]
Formula 6
N = 9.28×10-5ƒW
In Formula 6, “f” is the field source frequency in Hz, and “W” is the wide side length of the rectangular hole in cm.
B: Multiple Reflections Attenuation
Formula 7
B=20lg [1+2(N-1)/2(N+1)x10-0.1A]
In the case of high frequencies, the value after multiple reflection attenuation is extremely small and can be ignored.
K1: The correction coefficient of the number of meshes per unit area
Formula 8
K1 = -10lgSn (dB)
In Formula 8, “S” is the surface area of each mesh in square centimeters; “n” is the number of holes per square centimeter.
K2: The correction coefficient of low-frequency penetration
Formula 9
K2 = -20lg [1 + 35 / 1.15 (πCw2ƒσμ)]
= -20lg [1 + 35 / 1.15 (Cw /δ) -2]
In Formula 9, “Cw” is the diameter of the wire mesh; “δ” is the skin depth of the shield material; “ƒ” is the electromagnetic wave frequency; “σ” is the electrical conductivity of the shield; “μ” is the magnetic permeability of the shield.
In the case of high frequencies, the low-frequency penetration correction coefficient K2 is very small, and this value can still be regarded as 0 after formation.
K3: The correction coefficient of the mutual influence between adjacent meshes:
Formula 10
K3 = 20lg [1 / th (A / 8.686)]
In Formula 10, “A” is the absorption attenuation.
It can be seen from Formulas 4 and 5 that for good conductors such as copper, silver and aluminum, the larger the σ, the larger the R value. This shows that the shielding effectiveness in high-frequency electromagnetic fields mainly depends on the surface reflection attenuation, and the larger the σ of the metal, the better the shielding effectiveness. For high permeability materials such as iron and iron-nickel alloys, the larger the μ, the larger the A value. This shows that when the shielding material attenuates low-frequency electromagnetic fields, absorption attenuation will play a major role.
Therefore, the shielding materials used for low-frequency shielding must have good electrical conductivity, magnetic permeability, and must have sufficient thickness. It can be seen that for the near-field electric field source, the shielding effectiveness of the brass wire mesh should be higher than that of the stainless steel wire mesh, and for the near-field magnetic field source, the shielding effectiveness of the stainless steel wire mesh is higher than that of the brass wire mesh.
In the far-field shielding, the shielding effectiveness of brass and stainless-steel wire mesh should depend on the combination of absorption attenuation, reflection attenuation and various correction coefficient.
In the following chapter, we will analyze their shielding effectiveness in the far field in detail.
2. Calculation and Comparison of the Shielding Effectiveness of Stainless-Steel Wire Mesh and Brass Wire Mesh in Theory
The shielding effectiveness of stainless-steel wire mesh and brass wire mesh from 10MHz to 10GHz is calculated by the shielding effectiveness formula, respectively.
2.1. Calculate and compare the shielding effectiveness of stainless-steel wire mesh and brass wire mesh at the same mesh count, aperture, and wire diameter.
① 16 mesh (Table 2-1 and Table 2-2)
② 30 mesh (Table 2-3 and Table 2-4)
③ 80 mesh (Table 2-5 and Table 2-6)
Table 2-1 16 mesh
| Sample | Wire Diameter (mm) | Aperture (mm) |
| Stainless steel | 0.457 | 1.13 |
| Brass | 0.457 | 1.13 |
Table 2-2
| Frequency | 10MHz | 100MHz | 300MHz | 1GHz | 3GHz | 6GHz | 10GHz |
| Stainless steel | 76.75 | 59.61 | 46.81 | 39.85 | 29.87 | 23.91 | 19.97 |
| Brass | 79.25 | 59.82 | 46.86 | 39.86 | 29.88 | 23.91 | 19.97 |
Table 2-3 30mesh
| Sample | Wire Diameter (mm) | Aperture (mm) |
| Stainless steel | 0.305 | 0.54 |
| Brass | 0.305 | 0.54 |
Table 2-4
| Frequency | 10MHz | 100MHz | 300MHz | 1GHz | 3GHz | 6GHz | 10GHz |
| Stainless steel | 90.03 | 75.22 | 60.66 | 55.74 | 45.77 | 39.78 | 35.79 |
| Brass | 94.48 | 75.68 | 61.76 | 55.77 | 45.78 | 39.78 | 35.79 |
Table 2-5 80 mesh
| Sample | Wire Diameter (mm) | Aperture (mm) |
| Stainless steel | 0.165 | 0.15 |
| Brass | 0.165 | 0.15 |
Table 2-6
| Frequency | 10MHz | 100MHz | 300MHz | 1GHz | 3GHz | 6GHz | 10GHz |
| Stainless steel | 120.12 | 116.24 | 98.75 | 69.15 | 59.36 | 53.41 | 49.42 |
| Brass | 122.09 | 117.53 | 99.15 | 70.15 | 60.36 | 54.24 | 50.42 |
From the calculation data, it can be seen that the shielding effectiveness of stainless steel and brass wire mesh decreases with the increase of frequency, and the shielding effectiveness of wire mesh increases with the increase of mesh count.
In the case of stainless steel wire mesh and brass wire mesh with the same mesh count, wire diameter and aperture, the shielding effectiveness of brass wire mesh is slightly better than that of stainless steel wire mesh, and the gap becomes smaller and smaller as the frequency increases.
2.2. Calculation and comparison of shielding effectiveness of stainless steel and brass with the same mesh count and different wire diameters and apertures in practical application.
In actual production and engineering, due to the difference in mechanical properties and machining of materials, stainless steel and brass wire mesh with the same mesh are different in wire diameter and aperture. So, the shielding effectiveness of stainless steel and brass wire mesh in practical application is calculated and compared.
① 16 mesh (Table 3-7 and Table 3-8)
② 30 mesh (Table 3-9 and Table 3-10)
③ 80 mesh (Table 3-11 and Table 3-12)
Table 2-7 16 mesh
| Sample | Wire Diameter (mm) | Aperture (mm) |
| Stainless steel | 0.457 | 1.13 |
| Brass | 0.3 | 1.28 |
Table 2-8
| Frequency | 10MHz | 100MHz | 300MHz | 1GHz | 3GHz | 6GHz | 10GHz |
| Stainless steel | 76.75 | 59.61 | 46.81 | 39.85 | 29.87 | 23.91 | 19.97 |
| Brass | 70.02 | 54.69 | 42.84 | 32.06 | 21.45 | 17.97 | 13.68 |
Table 2-9 30 mesh
| Sample | Wire Diameter (mm) | Aperture (mm) |
| Stainless steel | 0.33 | 0.52 |
| Brass | 0.247 | 0.573 |
Table 2-10
| Frequency | 10MHz | 100MHz | 300MHz | 1GHz | 3GHz | 6GHz | 10GHz |
| Stainless steel | 90.03 | 75.22 | 65.66 | 55.74 | 51.61 | 45.59 | 41.16 |
| Brass | 85.42 | 67.16 | 57.27 | 47.29 | 43.13 | 37.12 | 32.70 |
Table 2-11 80 mesh
| Sample | Wire Diameter (mm) | Aperture (mm) |
| Stainless steel | 0.165 | 0.15 |
| Brass | 0.122 | 0.196 |
Table 2-12
| Frequency | 10MHz | 100MHz | 300MHz | 1GHz | 3GHz | 6GHz | 10GHz |
| Stainless steel | 120.12 | 116.24 | 98.75 | 69.15 | 59.36 | 53.41 | 49.42 |
| Brass | 114.63 | 112.82 | 91.57 | 63.59 | 53.64 | 47.65 | 43.66 |
According to the actual wire diameter and aperture of stainless steel and brass wire mesh, stainless steel wire mesh and brass wire mesh with same mesh count, the shielding effectiveness of stainless steel is about 10dB higher than brass wire mesh, and when the mesh count is higher than 80, and the frequency is up to 10GHz, the shielding effectiveness of stainless steel wire mesh and brass wire mesh can be above 50dB, which can meet the general shielding requirements.
3. Laboratory Test
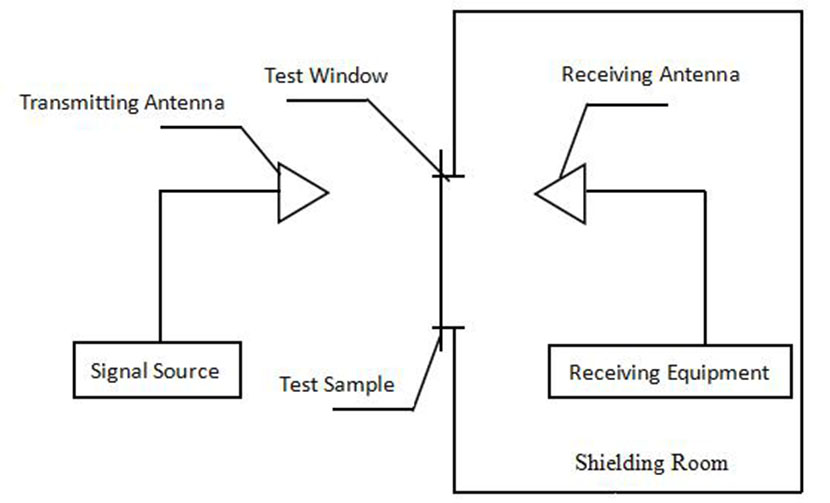
According to the shielding effectiveness measurement method of GB12190-90 in a high-performance shielding room, the shielding effectiveness test of stainless steel and brass wire mesh is carried out. The test principle is shown in the diagram below.
It can be seen from the diagram that the simulated interference source is placed outside the shielding room, and the test sample’s shielding effectiveness is the ratio of the electric field strength, magnetic field strength or power before and after it is placed in the shielding room window. The specification of the wire mesh tested is the same as the above specification.
The rules of the measured data are consistent with the calculation results. Due to the test being interfered a lot by the environment and testers, the test value will be 5-8dB lower than the calculated value.
Table 3-1 16 mesh
| Frequency | 10MHz | 100MHz | 300MHz | 1GHz | 3GHz | 6GHz | 10GHz |
| Stainless steel | 72.8 | 57.3 | 44.1 | 35.5 | 27.8 | 21.3 | 20.7 |
| Brass | 69.8 | 54.2 | 41.3 | 30.7 | 24.6 | 20.1 | 19.8 |
Table 3-2 30 mesh
| Frequency | 10MHz | 100MHz | 300MHz | 1GHz | 3GHz | 6GHz | 10GHz |
| Stainless steel | 87.9 | 72.4 | 61.5 | 50.7 | 46.3 | 42.8 | 37.6 |
| Brass | 85.4 | 70.2 | 56.7 | 46.5 | 41.7 | 38.5 | 32.9 |
Table 3-3 80 mesh
| Frequency | 10MHz | 100MHz | 300MHz | 1GHz | 3GHz | 6GHz | 10GHz |
| Stainless steel | 115.7 | 112.3 | 95.8 | 67.2 | 54.6 | 49.9 | 44.8 |
| Brass | 112.3 | 110.8 | 91.9 | 66.4 | 51.3 | 45.6 | 42.7 |
4. Conclusion
In the near field, shielding is divided into electric field shielding and magnetic field shielding, which should be considered separately.
For electric field shielding, reflection attenuation is the main factor, so shielding materials with high conductivity should be used. The electrical conductivity of brass is much higher than that of stainless steel, so the electric field shield should use brass.
For the magnetic field shielding, the absorption attenuation is very small, and the wave impedance of the magnetic field wave is very low, which determines that the reflection attenuation is also very small. When both of these parts are very small, the overall shielding effectiveness will be very low. So, shielding materials with high permeability should be used to increase absorption attenuation. The magnetic permeability of stainless steel is much higher than that of brass, so stainless steel should be used for magnetic field shielding.
In the far field, it is mainly the shielding of plane waves. In this condition, the shielding effectiveness of the shielding material must consider the effects of absorption attenuation and reflection attenuation.
In this paper, it is found that if the stainless steel and brass wire mesh are in the same specification, only considering the material difference, the shielding effectiveness of brass wire mesh is slightly better than that of stainless-steel wire mesh.
However, in actual application due to the influence of processing and other properties, stainless steel and brass wire mesh with the same mesh count are different in wire diameter and aperture. In this condition, the shielding effectiveness of stainless-steel wire mesh is better than that of brass wire mesh.
If you are looking for the electromagnetic wave shielding material, no matter stainless steel wire mesh, brass wire mesh, copper wire mesh and silver wire mesh, please click here to send us an inquiry.